Question

`\blue{\boxed{\boxed{\sf\blue{HELP ME PLEASE}}}}`
​

Answer 1

The completed two column proof is presented as follows;

Statement
`{}` Reason

1. AC bisects ∠A and ∠C
`{}` 1. Given

2. ∠ACB ≅ ∠ACD
`{}` 2. Definition of bisector

3. ∠BAC ≅ ∠DAC
`{}` 3. Definition of bisector

4.
`\overline {AC}` =
`\overline {AC}`
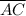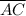
`{}` 4. Reflexive PE

5.
`\overline {AC}` ≅
`\overline {AC}`
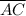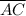
`{}` 5. Segments with equal lengths are congruent

6. ΔABC ≅ ΔADC
`{}` 6. By ASA

Explanation:

The completed two column proof is presented as follows;

Statement
`{}`

1. AC bisects ∠A and ∠C; The given data on the figure

2. ∠ACB ≅ ∠ACD;
`{}` A bisected angle is divided into two equal angles which are congruent to each other

3. ∠BAC ≅ ∠DAC
`{}` 3. Definition of bisector

4.
`\overline {AC}` =
`\overline {AC}`
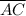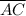
`{}` 4. Reflexive Property of Equality (PE)

5.
`\overline {AC}` ≅
`\overline {AC}`
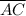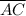
`{}` 5. Segments with equal lengths are congruent

6. ΔABC ≅ ΔADC
`{}` 6. By Angle-Side-Angle, ASA, is a condition for congruency of two triangles

Where two angles and the included side between the two angles on one triangle are equal to two angles and the included side between the two angles on another triangle, the two triangles are said to be congruent by the Angle-Side-Angle ASA rule and therefore, they each have equal measures for all corresponding angles sides.