Question

Can someone pls do these quick

Answer 1

6. x° is approximately 21.04°

7. x° is approximately 39.56°

8. x° is approximately 58.03°

9. x° is approximately 72.85°

Explanation:

6. In the given right triangle (a triangle with the measure of one of the interior angles equal to 90°, indicated by the small square between two sides) , we have;

The hypotenuse side length = 15

The adjacent side to the given reference angle, x° = 14

By trigonometric ratio, we have;

`cos\angle X = (Adjacent\ leg \ length)/(Hypotenuse \ length)`

`\therefore cos(x^(\circ)) = (14)/(15)`

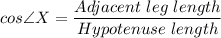
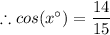
To find the value of x°, we make use of the inverse cosine function, arccos found on a scientific calculator, as follows;

x° = arccos(14/15) ≈ 21.04°

x° ≈ 21.04°

7. In the given right triangle, we have;

The length of the opposite side to the given reference angle, x° = 19

The length of the adjacent side to the given reference angle, x° = 23

By trigonometric ratios, we have;

`Tan(\angle X) = (Opposite \, side \ length)/(Adjacent\, side \ length)`

`\therefore tan(x^(\circ)) = (19)/(23)`

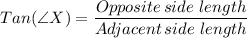
Therefore;

x° = arctan(19/23) ≈ 39.56°

x° ≈ 39.56°

8. In the given right triangle, the adjacent side to the reference angle, x° and the hypotenuse side are given, therefore, we have;

x° = arccos(9/17) ≈ 58.03°

x° ≈ 58.03°

9. The opposite side to the reference angle and the hypotenuse side are given

By trigonometric ratio, we have;

`sin\angle X = (Opposite \ leg \ length)/(Hypotenuse \ length)`

`\therefore sin(x^(\circ)) = (43)/(45)`

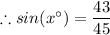
x° = arcsin(43/45) ≈ 72.85°

x° ≈ 72.85°.