Question

a charge of 2 * 10^-9C is placed at the origin, and another charge of 4 * 10^-9C is placed at x = 1.5m. find the point between these charges where a charge of 3 * 10^-9C should be placed so that the net electric force on it is zero

Answer 1

x₁ = 0.62 m

Step-by-step explanation:

In this exercise the force is electric, given by Coulomb's law

F =
`k (q_1q_2)/(r^2)`

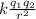
This force is a vector, since the three charges are in a line we can reduce the vector sum to a scalar sum.

For the sense of force let us use that charges of the same sign repel and charges of the opposite sign attract.

∑ F = F₁₂ - F₂₃

They ask us to find the point where the summaries of the force is zero.

F₁₂ - F₂₃ = 0

F₁₂ = F₂₃

let's fix a reference system located in the first charge (more to the left), the distance between the two charges is d = 1.5 m and x is the distance to the location of the second sphere

k q₁q₂ / x² = k q₂q₃ / (d-x) ²

q₁ (d-x) ² = q₃ x²

let's solve

d² - 2 x d + x² =
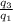`(q_3)/(q_1)` x²

x² (1 -
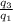`(q_3)/(q_1)`) - 2x d + d² = 0

we substitute the values

x² (1- 4/2) - 2 1.5 x + 1.5² = 0

x² (-1) - 3.0 x + 2.25 = 0

x² + 3 x - 2.25 = 0

let's solve the quadratic equation

x = [-3 ±
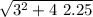`√( 3^2 + 4 \ 2.25)`] / 2

x = [-3 ± 4.24] / 2

x₁ = 0.62 m

x₂ = 3.62 m

since it indicates that the charge q₂ e places between the spheres, the correct solution is

x₁ = 0.62 m