Question

Helpppppppppppppppppppp

Answer 1

Given:

A rectangle with sides 40 and 25.

A circle with radius 8 inside the rectangle.

The area of circle is unshaded.

To find:

The probability that a point (randomly selected) will lie in the unshaded region.

Solution:

The area of the rectangle is:

`A_1=Length* Width`

`A_1=40* 25`

`A_1=1000`

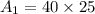
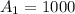
The area of the circle is:

`A_2=\pi r^2`

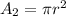
Where, r is the radius.

`A_2=\pi (8)^2`

`A_2=\pi (64)`

`A_2=64\pi`

`A_2\approx 201.06`

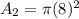
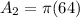
The probability that a point (randomly selected) will lie in the unshaded region is:

`\text{Probability}=\frac{\text{Unshaded region}}{\text{Total region}}`

`\text{Probability}=(A_2)/(A_1)`

`\text{Probability}=(201.06)/(1000)`

`\text{Probability}=0.20106`

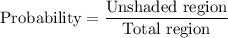
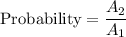
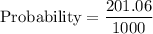
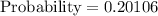
Therefore, the required probability is 0.20106.