Answer:
A=16.3 ft²
Explanation:
we are given a composite figure, composing of a triangle and a semicircle
first, let's find the area of the triangle
we are given the height (5 ft) and the base of the triangle (4 ft)
the formula for the area of the triangle is given as bh/2, where b is the base and h is the height
substitute the known values into the formula
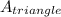 =bh/2
=bh/2
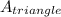 =(5*4)/2
=(5*4)/2
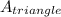 =20/2=10 ft²
=20/2=10 ft²
so the area of the triangle is 10 ft²
now to find the area of the semicircle:
the area of a semicircle is half the area of a circle; the area of a circle is given as πr², where r is the radius. Therefore, the area of a semicircle is (πr²)/2
4 ft isn't just the base of the triangle; it's also the diameter of the semicircle
however, we need the radius
the radius is half the diameter value
r=d/2
r=4/2
r=2 ft
so the radius is 4 feet
now find the area of the semicircle. Don't substitute for π just yet.
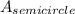 =(πr²)/2
=(πr²)/2
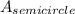 =(π*2²)/2
=(π*2²)/2
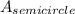 =4π/2
=4π/2
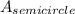 =2π
=2π
π is often substituted as 3.14 or 22/7
so if we used 3.14 for instance:
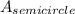 =6.28; rounded to the nearest tenth, that's 6.3 ft²
=6.28; rounded to the nearest tenth, that's 6.3 ft²
now add the two areas together to get the area of the composite figure
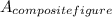 =
=
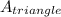 +
+
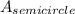
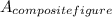 =10+6.3=16.3 ft²
=10+6.3=16.3 ft²
Hope this helps! Good luck on your assignment!!