Question

A reporter for a student newspaper is writing an article on the cost of off-campus housing. A sample was selected of 10 one-bedroom units within a half-mile of campus and the rents paid. The sample mean is $550 and the sample standard deviation is $60.05. Provide a 95% confidence interval estimate of the mean rent per month for the population of one-bedroom units within a half-mile of campus. Assume that population is normally distributed.

Answer 1

(507.05, 592.95)

Explanation:

Given data:

sample mean = $550, sample standard deviation S = $60.05

95% confidence interval , n = 10

For 95% confidence interval for the mean

mean ± M.E.

where M.E. is margin of error =
`t_(n-1), \alpha/2*(S)/(√(n) )`

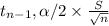
Substituting the values in above equation

`=t_(10-1), 0.05/2*(60.05)/(√(10) )`

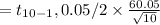
= 2.62×18.99

=42.955

= 550±42.95

=(507.05, 592.95)