Question

Factorize 2mh-2nh-3mk+3nk ​

Answer 1

`(2h-3k)(m-n)`

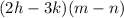
Explanation:

So we start with:

`2mh-2nh-3mk+3nk`

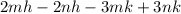
To make this look more managable, lets seperate this into two binomials. Lets start with:

`2mh-2nh`

So how can we factor this? Lets look at what both the values have in common.

We immediatly see that they both have a coefficent of 2.

They also both have a h.

This means we can factor out a 2h from both and get:

`2h(m-n)`

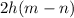
Now lets move onto the other binomial we had:

`-3mk+3nk`

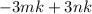
Again, we can immediatly see that both values in this binomial have a 3.

Be careful however, make sure to factor out a -3, not a 3.

Another thing the two values have in common is a k.

This means we can factor out -3k to get:

`-3k(m-n)`

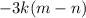
Now lets reintroduce our first factored binomial back into this equation:

`2h(m-n)-3k(m-n)`

Notice that both factored binomials have (m-n)

Because of this we can neaten up our equation into:

`(2h-3k)(m-n)`

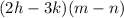
How does this work?

Recall that the -3k will distrubute, or in otherwords multiply the (m-n) as
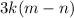`3k(m-n)`. It works the same way in this form as well, since when you use foil, you multiply 2h by both m and -n, and -3k by m and -n.

And we see, if we multiply the binomials out again, we get:

`(2h-3k)(m-n) = 2mh-2nh-3mk+3nk`

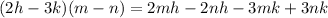
So our answer is:

`(2h-3k)(m-n)`

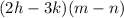
Hope this helps! :3

Answer 2

(2h-3k)(m-n)

Explanation:

factor by grouping, you can group the first two terms and the last two terms:

2h(m-n) + (-3k)(m-n)

there will be one factor in common, use that factor in combination with the factors that are not duplicated:

(2h-3k)(m-n)