Question

The current stock price of Alcoa is $25, and the stock does not pay dividends. The instantaneous risk-free rate of return is 4%. The instantaneous standard deviation of Alcoco's stock is 30%. You want to purchase a put option on this stock with an exercise price of $30 and an expiration date 30 days from now. According to the Black-Scholes OPM, you should hold __________ shares of stock per 100 put options to hedge your risk.

Answer 1

≈66 shares

Step-by-step explanation:

Given data:

Current price ( S ) = $25

strike price ( K ) = $30

risk free rate ( r ) = 4% = 0.04

Standard deviation ( std ) = 30% = 0.3

In( s/k ) = In ( 25/30 ) = -0.1827

t = 30 / 365

To determine the number of shares of stock per 100 put options to hedge the risk we will apply the relation below

Number of shares to hedge risk = | N(d1) - 1 | * 100 ----- ( 1 )

where :

`d1 = (In((s)/(k)) + ( r +(std^2)/(2))*t )/(std√(2) )`

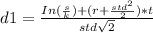
N(d1 ) = cumulative distribution function = 0.3394

back to equation 1 = 0.6606 * 100 = 66 shares

attached below is the remaining part of the solution