Question

Write a formula for the function g(x) obtained when the graph of f(x) = 1/x is shifted down 4 units and to the right 6 units .

Please help !!!!
*NO LINKS*

Answer 1

Answer:
`g(x) = (1)/(x-6) - 4`

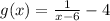
This can be written out as g(x) = 1/(x-6) - 4

The "x-6" is in the denominator, while the "-4" is not.

=============================================================

Step-by-step explanation:

We'll start with the parent function
`f(x) = (1)/(x)`

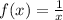
When we shift 4 units down, we're subtracting 4 from the y coordinate of each point on the curve. Which is the same as subtracting 4 from f(x) because y = f(x).

So we have
`h(x) = f(x) - 4 = (1)/(x) - 4` as an intermediate step.

Then to shift 6 units to the right, we'll replace every x with "x-6". Imagine we kept the h(x) curve completely still, and instead we moved the xy axis 6 units to the left. This would give the illusion of h(x) moving 6 units to the right if we made the xy axis stay still. So that's why we go for "x-6" instead of "x+6".

Therefore, we end up with
`g(x) = (1)/(x-6) - 4`

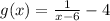
Side note: plugging in x = 6 leads to a division by zero error. This would mean x = 6 is not in the domain.