Question

A standard parallel plate capacitor is connected to a battery and is given enough time to charge fully. After it is fully charged, the capacitor is disconnected from the battery. After that, prankster Bob comes along and pulls the plates further apart from each other, doubling the distance d between the plates. How do the following quantities change? The choices are: quadruple, double, stay the same, halve, or quarter.

a) Capacitance
b) Charge on the capacitor
c) Voltage across the capacitor
d) Electric field within the capacitor
e) Energy stored in the capacitor
f) Does Bob have to do work in order to pull the plates apart? (Yes or no, and a brief explanation)
g) Are parts (e) and (f) consistent, given that the battery was disconnected?

Answer 1

a) capacitance is doubled., b) Q = cte, c) oltage doubling the distance doubles, d) ΔE =0, e) U = Q² / 2C, f) W>0

Step-by-step explanation:

he capacitance of a condensate is

C =
`( Q)/( \Delta V) =\epsilon_o (A)/(d)`

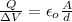
let's use this expression to answer the question

a) Capacitance.

Without distance, the capacitance is doubled.

Answer: Half

b) The charge.

As the battery is disconnected, no more electrons reach the capacitor, so the charge remains the same

Q = cte

c) the voltage

ΔV = E d = (
`((Q)/(\epsilon_o A)) \ d`

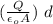
so the voltage doubling the distance doubles

d) The electric field between parallel plates is constant

E = Q / A eo

E =0

e) The stored energy is described by the expression

U = Q² / 2C

as capacitance decreases and discant increases, stored energy increases

f) The work to separate the positive charge, that the force must be in the same direction as the electric force

g) when the battery is disconnected the energy in the capacitor remains constant