Question

The area of a square garden is 900 square feet. What is the length of one side of the garden? A 450 ft C 225 ft B 300 ft D 30 ft​

Answer 1

Explanation:

Area of square garden=a^2

ATQ

➝a^2=900 sq.feet

➝a=√900

➝a=30feets

Correct option-D

Answer 2

`\boxed {\boxed {\sf D. \ 30 \ feet}}`

Explanation:

The area of a square is found by multiplying the base and the height, but since all the sides are equal, it is equal to multiplying a side by another side.

`a=s*s`

`a=s^2`

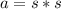
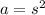
We know the square garden has an area of 900 square feet. We can substitute this value in for a.

`900 \ ft^2=s^2`

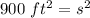
Since we are solving for the side, we have to isolate the variable s. It is being squared. The inverse of a square is the square root, so we take the square root of both sides.

`\sqrt {900 \ ft^2}= √(s^2)`

`\sqrt {900 \ ft^2}=s \\`

`30 \ ft=s`

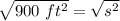
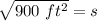
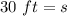
One side of the garden is equal to 30 feet and choice D is correct.