Question

In a chess club the probability that Shaun will beat Mike is 3/8 .

The probability that Shaun will beat Tim is 5/7 .
(Assume all the games are independent of one another)
If Shaun plays 1 game with Mike and then 1 game with Tim, what is the probability that Shaun loses both games?

Answer 1

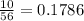`(10)/(56) = 0.1786` probability that Shaun loses both games

Explanation:

Games are independent, so we find each separate probability, and multiply them.

In a chess club the probability that Shaun will beat Mike is 3/8.

So
`1 - (3)/(8) = (8)/(8) - (3)/(8) = (5)/(8)` probability that Shaun loses.

The probability that Shaun will beat Tim is 5/7 .

So
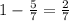`1 - (5)/(7) = (2)/(7)` probability that Shaun loses.

What is the probability that Shaun loses both games?

This is:

`p = (5)/(8) * (2)/(7) = (5*2)/(8*7) = (10)/(56) = 0.1786`

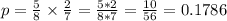
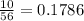`(10)/(56) = 0.1786` probability that Shaun loses both games