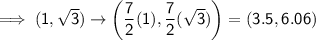Question

circle c shown below was dilated with the origin as the center of dilation to create circle C' which rule represents the transformation?

Answer 1

• A. (x, y) → (2/7x, 2/7y)

Explanation:

Equation of the smaller circle:

• x² + y² = 2²

Equation of the greater circle:

• x² + y² = 7²

The scale factor is the ratio of radiuses:

• k = r₁ / r₂ = 2/7

So the rule is:

• (x, y) → (kx, ky) = (2/7x, 2/7y)

Correct choice is A

Answer 2

`\sf A. \quad (x, y) \rightarrow \left((7)/(2)x, (7)/(2)y \right)`

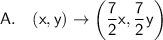
Explanation:

The distance from the center of the circle to any point on the circumference is the radius.

From inspection of the given graph:

• Radius of Circle C (before dilation) = 2 units
• Radius of Circle C' (after dilation) = 7 units

To find the scale factor of the dilation from the small circle C to the large circle C', divide the radius of the large circle by the radius of the small circle.

Therefore, the dilation is an enlargement of scale factor ⁷/₂ about the origin.

So the rule that represents the transformation is:

`\sf (x, y) \rightarrow \left((7)/(2)x, (7)/(2)y \right)`

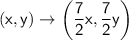
Check (see attached):

Point (0, 2) is on circle C.

`\implies \sf (0, 2) \rightarrow \left((7)/(2)(0), (7)/(2)(2) \right)=(0,7)`

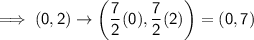
Point (1, √3) is on Circle C:

`\implies \sf (1, √(3)) \rightarrow \left((7)/(2)(1), (7)/(2)(√(3)) \right)=\left(3.5,6.06)`