Question

Based on past experience, the daily revenue, X, for a coffee shop in a city is a normally distributed random variable with a mean daily revenue of $900. The first co-owner of the shop feels that the shop is known throughout the city and as such they could reduce the amount of money spent on advertising without causing a decrease in the population mean daily revenue. The second co-owner is concerned that a reduction in advertising would in fact result in a decrease in the population mean daily revenue. To settle the issue, the first co-owner decides to decrease the advertising dollars for a period of time, during which she will select 64 days at random and compute the sample mean daily revenue. She will then perform a hypothesis test to determine if the sample mean daily revenue provides significant evidence to conclude that the population mean daily revenue is less than $900 when the advertising dollars are reduced. The first co-owner observes a sample mean daily revenue of $892.50 with a sample standard deviation of $24 when the advertising dollars have been reduced. What is the p-value for her test

Answer 1

The p-value for her test is 0.0075.

Explanation:

She will then perform a hypothesis test to determine if the sample mean daily revenue provides significant evidence to conclude that the population mean daily revenue is less than $900 when the advertising dollars are reduced.

At the null hypothesis, we test that the mean is less than 900, that is:

`H_0: \mu = 900`

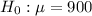
At the alternate hypothesis, we test that the mean is less than 900, that is:

`H_a: \mu < 900`

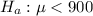
The test statistic is:

We have the standard deviation for the sample, which means that the t-distribution is used to solve this question.

`t = (X - \mu)/((s)/(√(n)))`

In which X is the sample mean,
`\mu` is the value tested at the null hypothesis, s is the standard deviation of the sample and n is the size of the sample.

900 is tested at the null hypothesis:

This means that
`\mu = 900`

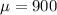
Sample of 64 days. The first co-owner observes a sample mean daily revenue of $892.50 with a sample standard deviation of $24 when the advertising dollars have been reduced.

This means that
`n = 64, X= 892.50, s = 24`

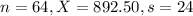
Value of the test:

`t = (X - \mu)/((s)/(√(n)))`

`t = (892.50 - 900)/((24)/(√(64)))`

`t = -2.5`

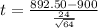
What is the p-value for her test?

The pvalue of the test is the probability of a sample mean below 892.5, which is a left-tailed test for t = -2.5 with 64 - 1 = 63 degrees of freedom.

Using a calculator, the p-value for her test is 0.0075.