9514 1404 393
Answer:
12. 13
14. A
15. B
Explanation:
I choose to work 3 problems to show how multiplication and division work with exponents.
__
12. You are looking for the coefficient of the x² term. It will be the sum of the coefficients of partial products that result in the variable being x². Those partial products will be of the form (ax²)(b) or (ax)(bx).
We note there are both x² and x terms in the first factor, but only x terms in the second factor. So, the x² term of the product will be ...
(2x²)(4) +(5x)(x) = (8 +5)x² = 13x²
The missing coefficient is 13.
__
14. The rules of exponents are ...
(a^b)(a^c) = a^(b+c)
(a^b)^c = a^(bc)
(a^b)/(a^c) = a^(b-c)
The given expressions can be simplified as ...
Koby
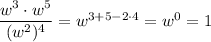
Paulo
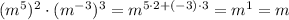
Kobe Only wrote an expression equivalent to 1.
__
15. The given expression is of the form
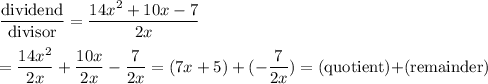
The true statement is ...
the quotient has a remainder of -7/(2x)
__
Additional comment
Strictly speaking, a division problem can be expressed as ...
dividend = (divisor)(quotient) + remainder
In this instance, this would be ...
14x² +10x -7 = (2x)(7x +5) -7
which is to say that -7 is the remainder. The term -7/(2x) is actually part of the quotient.
The above (quotient) + (remainder) should actually be ...
(quotient) +(remainder)/(divisor)
You will notice the answer choices have the terms "dividend" and "divisor" swapped, and that the degree of the binomial quotient is 1, not 2. Thus the only choice that begins to make sense is the one highlighted above--even though it, too, is technically incorrect.