Question

State your conclusion to the following hypothesis test.

A certain academic program boasts that 87% of their graduates find full-time employment in their field within the first year of graduation. The academic director is concerned that market factors may have adversely affected the full-time placement rate and decides to perform a Hypothesis Test to see if her concern is warranted.

The hypothesis test is performed at a 5% significance level and the resulting p-value is 0.07.

Assume that all conditions for testing have been met and choose the statement that contains the correct conclusion.

Question 11 options:

a.there is not sufficient sample evidence to conclude that the full-time placement rate is now less than 87% because the p-value is greater than 0.05.

b.there is sufficient sample evidence to conclude that the full-time placement rate is now less than 87% because the p-value is greater than 0.05.

c.there is sufficient sample evidence to conclude that the full-time placement rate is 87% because the p-value is greater than 0.05.

c.there is not sufficient sample evidence to conclude that the full-time placement rate is 87% because the p-value is greater than 0.05.

Construct the equation of the regression line.

An editing firm compiled the following table which lists the number of pages contained in a piece of technical writing and the cost of proofreading and correcting them (in dollars). Assume there is a significant linear relationship between X and Y and construct the equation of the linear regression line.


Number of Pages, x
7
12
4
14
25
30

Cost, y
128
213
75
250
446
540
Question 28 options:

yˆ=17.9(x)+1.6

yˆ=15.4(x)+7.1

yˆ=1.6(x)+17.9

yˆ=7.1(x)+15.4

Use the model to make the appropriate prediction.

A sociologist wanted to determine whether there was a relation between a state's poverty rate (x) and its teen pregnancy rate (y). Data from all 50 states produced the regression model:

yˆ=4.3+1.4(x)

What does the model suggest for the poverty rate of Florida, which has a poverty rate of 16.6?

Answer 1

Part A

a. There is not sufficient sample evidence to conclude that the full-time placement rate is now less than 87% because the p-value is greater than 0.05

Part B

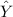`\hat Y` = 17.9·(x) + 1.6

Part C

The teen pregnancy rate in Florida is 6.54

Explanation:

The percentage of graduates that find full-time employment in their fields within the first year of graduation = 87%

The significant level of the hypothesis test = 5% = 0.05

The p-value = 0.07

Given that the testing conditions are met, we have;

The p-value is larger than the significant level of 0.05, therefore, it cannot be concluded that there is significant difference between the two rates

Therefore;

There is not enough statistical evidence available to come to a conclusion that the placement rate of full-time students has reduced below the given 87% because from the statistics, the p-value is larger than 0.05.

Part B

Number of Pages, x; 7, 12, 4, 14, 25, 30

Cost, y; 128, 213, 75, 250, 446, 540

The regression analysis formula is;

Y = a + b·X

We have;

`b = (N\sum XY - \left (\sum X \right )\left (\sum Y \right ))/(N\sum X^(2) - \left (\sum X \right )^(2))`

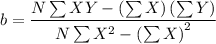
∴ b = (6×34602-92×1652)/(6×1930 - 92²) ≈ 17.852

`a = (\sum Y - b\sum X)/(N)`

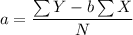
a = (1652 - 17.852 × 92)/6 ≈ 1.6

∴ Y ≈ 17.9·(x) + 1.6

Part C

The given regression model is y = 4.3 + 1.4(x)

Therefore, at x = 1.6, we get;

y = 4.3 + 1.4 × 1.6 = 6.54

The suggests that the teen pregnancy rate in Florida is 6.54.