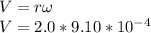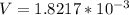Answer:
a)
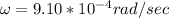
b)
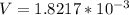
Step-by-step explanation:
From the question we are told that:
Mass of woman
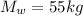
Radius of merry go round
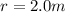
Rotational inertia
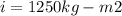
Mass of rock
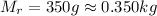
Speed of rock
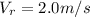
Tangent angle to the outer edge
a)
Generally the equation for conservation of momentum is mathematically given by
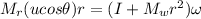
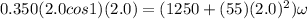
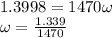
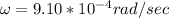
b)
Generally the equation for linear speed V is mathematically given by