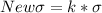Answer:
(a)
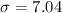
(b)
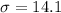
(c) The population standard deviation is multiplied by k
Explanation:
Given
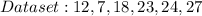
Solving (a): The population standard deviation
Start by calculating the mean
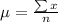
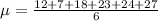
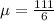
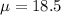
The population standard deviation is:
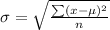
This gives:
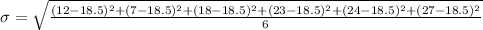
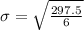
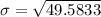
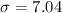
Solving (b): Double the dataset and calculate the new population standard deviation
The new dataset is:
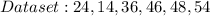
Start by calculating the mean
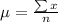
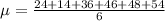
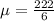
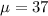
The population standard deviation is:
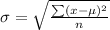
This gives:
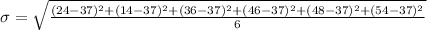
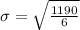
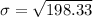
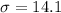
Solving (c): What happens when the dataset is multiplied by k
In (a), we have:
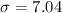
In (b), when the dataset is doubled,
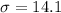
This implies that when the dataset is multiplied by k, the population standard deviation will be multiplied by the same factor:
i.e.