9514 1404 393
Answer:
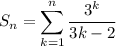
Explanation:
The sequence terms appear to have numerators that are powers of 3, and denominators that are a linear (arithmetic) sequence with a first term of 1 and a common difference of 3.
numerator: 3^x
denominator: 1 +3(n -1) = 3n-2
Then the sum of n terms of the sequence can be described by ...
