Question

Solid fats are more likely to raise blood cholesterol levels than liquid fats. Suppose a nutritionist analyzed the percentage of saturated fat for a sample of 6 brands of stick margarine (solid fat) and for a sample of 6 brands of liquid margarine and obtained the following results: Exam Image Exam Image We want to determine if there a significant difference in the average amount of saturated fat in solid and liquid fats. What is the test statistic

Answer 1

`t = 31.29`

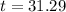
Explanation:

Given

`\begin{array}{ccccccc}{Stick} & {25.8} & {26.9} & {26.2} & {25.3} & {26.7}& {26.1} \ \\ {Liquid} & {16.9} & {17.4} & {16.8} & {16.2} & {17.3}& {16.8} \ \end{array}`

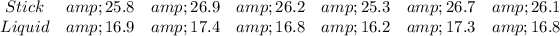
Required

Determine the test statistic

Let the dataset of stick be A and Liquid be B.

We start by calculating the mean of each dataset;

`\bar x =(\sum x)/(n)`

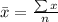
n, in both datasets in 6

For A

`\bar x_A =(25.8+26.9+26.2+25.3+26.7+26.1)/(6)`

`\bar x_A =(157)/(6)`

`\bar x_A =26.17`

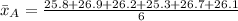
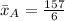
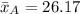
For B

`\bar x_B =(16.9+17.4+16.8+16.2+17.3+16.8)/(6)`

`\bar x_B =(101.4)/(6)`

`\bar x_B =16.9`

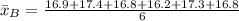
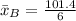
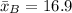
Next, calculate the sample standard deviation

This is calculated using:

`s = \sqrt{(\sum(x - \bar x)^2)/(n-1)}`

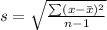
For A

`s_A = \sqrt{(\sum(x - \bar x_A)^2)/(n-1)}`

`s_A = \sqrt{((25.8-26.17)^2+(26.9-26.17)^2+(26.2-26.17)^2+(25.3-26.17)^2+(26.7-26.17)^2+(26.1-26.17)^2)/(6-1)}`

`s_A = \sqrt{(1.7134)/(5)}`

`s_A = √(0.34268)`

`s_A = 0.5854`

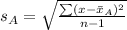
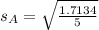
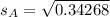
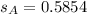
For B

`s_B = \sqrt{(\sum(x - \bar x_B)^2)/(n-1)}`

`s_B = \sqrt{((16.9 - 16.9)^2+(17.4- 16.9)^2+(16.8- 16.9)^2+(16.2- 16.9)^2+(17.3- 16.9)^2+(16.8- 16.9)^2)/(6-1)}`

`s_B = \sqrt{(0.92)/(5)}`

`s_B = √(0.184)`

`s_B = 0.4290`

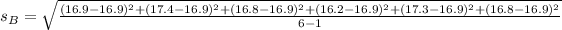
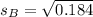
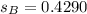
Calculate the pooled variance

`S_p^2 = ((n_A - 1)*s_A^2 + (n_B - 1)*s_B^2)/((n_A+n_B-2))`

`S_p^2 = ((6 - 1)*0.5854^2 + (6 - 1)*0.4290^2)/((6+6-2))`

`S_p^2 = (2.6336708)/(10)`

`S_p^2 = 0.2634`

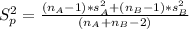
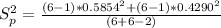
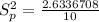
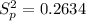
Lastly, calculate the test statistic using:

`t = ((\bar x_A - \bar x_B) - (\mu_A - \mu_B))/(√(S_p^2/n_A +S_p^2/n_B))`

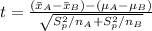
We set

`\mu_A = \mu_B`

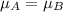
So, we have:

`t = ((\bar x_A - \bar x_B) - (\mu_A - \mu_A))/(√(S_p^2/n_A +S_p^2/n_B))`

`t = ((\bar x_A - \bar x_B) )/(√(S_p^2/n_A +S_p^2/n_B))`

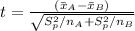
The equation becomes

`t = ((26.17 - 16.9) )/(√(0.2634/6 +0.2634/6))`

`t = (9.27)/(√(0.0878))`

`t = (9.27)/(0.2963)`

`t = 31.29`

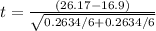
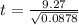
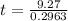
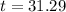
The test statistic is 31.29