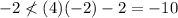9514 1404 393
Answer:
A) The first inequality has a dashed boundary line with a slope of 4 and a y-intercept of -2. The shading is below the line. The second inequality has a solid boundary line with a slope of 5/2 and a y-intercept of -2. The shading is above the line. The solution space is a narrow wedge extending up and to the right of the y-intercepts at (0, -2) through the fourth quadrant into the first quadrant.
B) Not in the solution space. The point does not satisfy y < 4(-2) -2 because -2 is not less than -10.
Explanation:
Part A:
The boundary line of each inequality is in slope-intercept form, so can be drawn easily by finding points with the appropriate slope=rise/run from the common y-intercept at (0, -2).
The first inequality does not include the "or equal to" case, so the boundary line will be dashed. The relation of y and the inequality symbol is y < ( ), so the shading will be below the line, where y-values are less than those on the line.
The second inequality includes the "or equal to" case, so the boundary line is solid. The relation of y and the inequality symbol is y ≥ ( ), so the shading will be above the line, where y-values are greater than those on the line.
The two shaded areas overlap in a narrow wedge between lines with slope 2.5 and 4. The lower-left point of the wedge is the common y-intercept at (0, -2). It extends through the fourth quadrant into the first quadrant. This wedge is the solution area.
__
Part B:
Based on the above description, no part of the solution space is in the third quadrant, where the point (-2, -2) lies. The point is not in the solution space. It does not satisfy the first inequality: