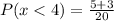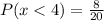Question

An employment agency required 20 secretarial candidates to type the same manuscript. The number of errors found in each manuscript is summarized in the histogram. Find the empirical probability that a candidate has less than four errors in the typed manuscript.

Answer 1

The probability that a candidate has less than 4 errors is 0.40

Explanation:

Given

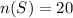`n(S)= 20` --- candidates

See attachment for histogram

Required

`P(x < 4)`

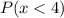
From the attached histogram, the errors less than 4 are: 0 or 1 and 2 or 3

And the corresponding frequencies are: 5 and 3, respectively.

So:

`P(x < 4) = P(0\ or\ 1) + P(2\ or\ 3)`

This gives:

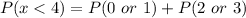
`P(x < 4) = (n(0\ or\ 1))/(n(S)) + (n(2\ or\ 3))/(n(S))`

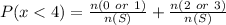
Substitute 5, 3 and 20 for n(0 or 1), n(2 or 3) and n(S), respectively

`P(x < 4) = (5)/(20) + (3)/(20)`

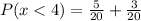
Take LCM

`P(x < 4) = (5+3)/(20)`

`P(x < 4) = (8)/(20)`

`P(x < 4) = 0.40`