Answer:
Magnitude: 3√10
Direction angle: 71.56°
Explanation:
The magnitude ||v|| of a vector <a,b>, would be:


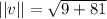

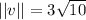
The vector's reference angle would be:
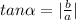
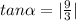
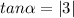
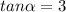
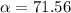
If
 is your reference angle, then your direction angle ∅ depends on what quadrant the vector is located in. Since <3,9> is located in Quadrant I, then ∅=
is your reference angle, then your direction angle ∅ depends on what quadrant the vector is located in. Since <3,9> is located in Quadrant I, then ∅=
 , which means your direction angle is also 71.56°
, which means your direction angle is also 71.56°