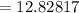Answer:
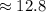
Explanation:
1. Approach
Assume that this problem is asking for the value of the shaded region.
To solve this problem, one must find the area of the entire circle. The measure of the arc around the shaded region is given, this measure can be used to find the fraction of the arc around the shaded region is, out of the entire circle. After doing so, multiply the fraction of the arc, by the area of the circle, to find the area of the shaded region.
2. Area of the circle
The formula to find the area of a circle is the following,
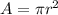
Where (
 ) represents the numerical value, (
) represents the numerical value, (
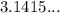 ), and (
), and (
 ) represents the radius of the circle. The radius of a circle is the distance from the center of the circle to the circumference of the circle, or the outside boundary of the circle.
) represents the radius of the circle. The radius of a circle is the distance from the center of the circle to the circumference of the circle, or the outside boundary of the circle.
Substitute in the given values and solve for the area,

3. Find the fraction that the shaded region takes up
It is given that the arc surrounding the shaded region has a measure of (
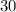 ). The central angles theorem states that if the vertex of an arc is the center on the center of the circle, then the measure of the surrounding arc is equal to the measure of the angle. Since there are (
). The central angles theorem states that if the vertex of an arc is the center on the center of the circle, then the measure of the surrounding arc is equal to the measure of the angle. Since there are (
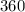 ) degrees in the full angle, then the fraction of the are is the measure of the arc over (
) degrees in the full angle, then the fraction of the are is the measure of the arc over (
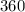 ). Use this to solve for the fraction that the angle takes up,
). Use this to solve for the fraction that the angle takes up,
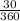
Simplify,
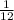
4. Find the area of the shaded region,
Now multiply the fraction that the arc takes up by the total area of the circle,
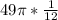
Multiply,

Convert to decimal form,