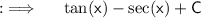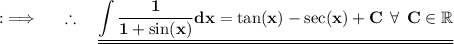We are given with a Indefinite integral , and we need to find it's value ,so , let's start
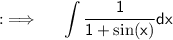
Now , Rationalizing the denominator i.e multiplying the numerator and denominator by the conjugate of denominator i.e 1 - sin(x)
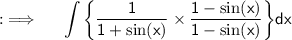
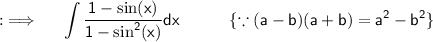

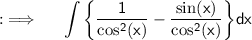
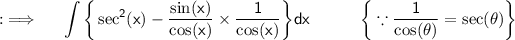
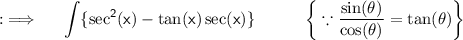
Now , we know that ;
Using this we have ;
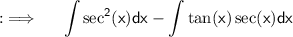
Now , we also knows that ;
Where C is the Arbitrary Constant . Using this