Answer:
Explanation:
We know the perimeter of a triangle is the sum of all the sides( two legs and one hypotenuse).
By pythagoras we know that
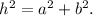
and the perimeter is
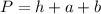 .
.
Since P=24 and a=6 we have these equations:
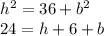
From the last equation we have
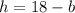 . Replace h in the first equation we get that
. Replace h in the first equation we get that
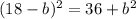
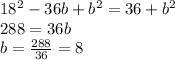
and h=18-8=10