Answer:
v = 1.98 m / s
Step-by-step explanation:
Let's analyze this exercise a bit, initially the hanging box is at a height h, which is why it has gravitational power energy, as the system is removing the kinetic energy is zero and just when the box reaches the floor its potential energy has dropped to zero and the three bodies have kinetic energy, also between the box and the horizontal surface there is friction, so there is work. Let's use the relationship between work and energy
starting point. Before starting the movement
Em₀ = U = m g h
final point. Just before the block hit the floor
Em_f = K = ½ M v² + ½ I w² + ½ m v²
the speed of the two blocks must be the same to maintain the tension of the rope
The work of the friction force
the friction force opposes the movement so its work is negative
W = - fr x
the law of equilibrium is the largest block
N-W = 0
N = W = Mg
we substitute
W = - μ M g x
the relationship between the work of the non-conservative force (friction) and the energy is
W = Em_f - Em₀
- μ Mg x = ½ M v² + ½ I w² + ½ m v² - mg h
the moment of inertia of a hollow sphere is
I = ⅔ m_s r²
angular and linear velocity are related
v = w r
w = v / r
the distance the horizontal block travels must be the same as the distance the vertical block travels
x = h
let's substitute
- μ M g h = ½ (M + m) v² + ½ (⅔ m_s r²) (v/r) ² - m g h
(- μ M + m) g h = ½ (M + m + ⅔ m_s) v²
v² =

let's calculate
v² = 2 (-0.15 7.6 +2.4) 9.8 0.61 / (7.6 + 2.4 + 2/3 1.2)
v =
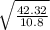
v = 1.98 m / s