Given:
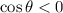 and
and
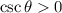
To find:
The quadrant in which θ lie if the given statements are true.
Solution:
We know that,
All trigonometric ratios are positive in I quadrant.
Only sine and cosecant are positive in II quadrant and others are negative.
Only tangent and cotangent are positive in III quadrant and others are negative.
Only cosine and secant are positive in IV quadrant and others are negative.
We have,
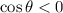 and
and
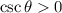
Here, cosine is negative and cosecant is positive. It is only possible when
 lies in II quadrant.
lies in II quadrant.
Therefore, the
 lies in II quadrant.
lies in II quadrant.