Question

Suppose you observe a star orbiting the galactic center at a speed of 1400 km/s in a circular orbit with a radius of 26 light-days. Calculate the mass of the object that the star is orbiting. Express your answer in solar masses to two significant figures.

Answer 1

M = 9.9 x 10⁶ Solar masses

Step-by-step explanation:

Here the centripetal force is given by the gravitational force between star and the object:

`Gravitational\ Force = Centripetal\ Force \\(mv^2)/(r) = (GmM)/(r^2)\\\\M = (v^2r)/(G)`

where,

M = Mass of Object = ?

v = orbital speed of star = 1400 km/s = 1400000 m/s

G = Universal Gravittaional Constant = 6.67 x 10⁻¹¹ N.m²/kg²

r = distance between star and object = (26 light-days)(2.59 x 10¹³ m/1 light-day) = 6.735 x 10¹⁴ m

Therefore,

`M = ((1400000\ m/s)^2(6.735\ x\ 10^(14)\ m))/(6.67\ x \ 10^(-11)\ N.m^2/kg^2)`

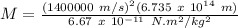
M = (1.97 x 10³⁷ kg)(1 solar mass/ 1.989 x 10³⁰ kg)

M = 9.9 x 10⁶ Solar masses