Answer:
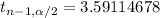
Therefore we do not have sufficient evidence at
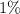 level that the true mean diameter has moved away from the target
level that the true mean diameter has moved away from the target
Explanation:
From the question we are told that:
Sample size

Mean diameter
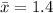
Standard deviation
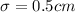
Null hypothesis
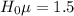
Alternative hypothesis
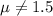
Significance level
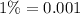
Generally the equation for test statistics is mathematically given by
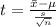
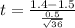

Therefore since this is a two tailed test
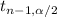
Where
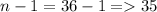

From table
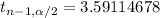
Therefore we do not have sufficient evidence at
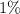 level that the true mean diameter has moved away from the target
level that the true mean diameter has moved away from the target