Question

When a low-pressure gas of hydrogen atoms is placed in a tube and a large voltage is applied to the end of the tube, the alors will emit electromagnetic radiation and visible light can be observed. If this light passes through a diffraction grating, the resulting spectrum appears as a pattern of four isolated, sharp parallel lines, called spectral lines. Each spectral line corresponds lo one specific wavelength that is present in the light emitted by the source. Such a discrete spectrum is referred to as a line spectrum

By the early 19th century, it was found that discrete spectra were produced by every chemical element in its gaseous slale. Even though these spectra were found to share the common feature of appearing as a set of isolated lines, it was observed that each element produces its own unique pattern of lines. This indicated that the light emitted by each element contains a specific set of wavelengths that is characteristic of that element.
part A What is the wavelength of the line corresponding to n =4 in the Balmer series? Express your answer in nanometers to three significant figures.
Part B What is the wavelength of the line corresponding to t=5 in the Balmer series? Express your answer in nanometers to three significant figures.

Answer 1

A) λ = 4.88 10² nm, B) λ = 4.08 10² nm

Step-by-step explanation:

The spectrum of hydrogen is correctly explained by the Bohr model, where the energy of each level is

Eₙ = -13.606 /n² [eV]

the transition generally occurs from a given level to a lower state nf <no, so a transition is

ΔE = E_f -Eₙ = -13,606 (
`(1)/(n_f^2) - (1)/(n_o^2)` )

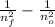to find the wavelength let's use the planck relation

ΔE = h f

the speed of light is

c = λ f

we substitute

ΔE = h c /λ

λ =
`(h \ c)/( \Delta \lambda)`

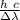
let's apply this equation to our case

the Balmer series has as final state the level n_f = 2

A) initial state n₀ = 4, final state n_f = 2

ΔE = -13.606 (
`(1)/(2^2) - (1)/(4^2)` )

ΔE = 2.55 eV

let's reduce to SI units

ΔE = 2.55 eV (1.6 10⁻¹⁹ J / 1 eV) = 4.08 10⁻¹⁹ J

we calculate

λ = 6.63 10⁻³⁴ 3 10⁸ / 4.08 10⁻¹⁹

λ = 4.875 10⁻⁻⁷ m

we reduce to nm

λ = 4.875 10⁻⁷ m (10⁹ nm / 1m)

λ = 487.5 nm

we reduce to three significant figures

λ = 4.88 10² nm

B) initial state n₀ = 5

ΔE = -13,606 (
`(1)/(2^2) - (1)/(5^2)` )

ΔE = 2,857 eV

we repeat the process of the previous point

ΔE= 2,857 1.6 10⁺¹⁹ = 4.286 10⁻¹⁹J

we look for the wavelength

λ = 6.63 10⁻³⁴ 3 10⁸ / 4.88 10⁻¹⁹

λ = 4.0758 10⁻⁷ m

we reduce to nm

λ = 4.0758 10² nm

ignificant numbers

λ = 4.08 10² nm