Answer:
The p-value of the test is 0.0018, which means that for a level of significance higher than this, there is sufficient evidence to claim that less than 50% of Internet users get their health questions answered online.
Explanation:
Test the claim that less than 50% of Internet users get their health questions answered online.
At the null hypothesis, we test that 50% of Internet users get their health questions answered online, that is:
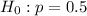
At the alternate hypothesis, we test that this proportion is less than 50%, that is:
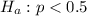
The test statistic is:

In which X is the sample mean,
 is the value tested at the null hypothesis,
is the value tested at the null hypothesis,
 is the standard deviation and n is the size of the sample.
is the standard deviation and n is the size of the sample.
0.5 is tested at the null hypothesis:
This means that
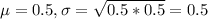
A random sample of 1318 Internet users was asked where they will go for information the next time they need information about health or medicine; 606 said that they would use the Internet.
This means that
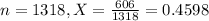
Test statistic:

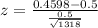
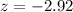
P-value of the test and decision:
The p-value of the test is the probability of finding a sample proportion below 0.4598, which is the p-value of z = -2.92.
Looking at the z-table, z = -2.92 has a p-value of 0.0018.
The p-value of the test is 0.0018, which means that for a level of significance higher than this, there is sufficient evidence to claim that less than 50% of Internet users get their health questions answered online.