Given:
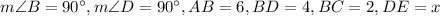 .
.
To find:
The value of x.
Solution:
In triangles ABC and ADE,
 (Right angles)
(Right angles)
 (Common angles)
(Common angles)
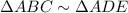 (AA property of similarity)
(AA property of similarity)
We know that the corresponding sides of similar triangles are proportional. So,
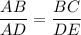
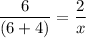
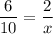
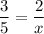
On cross multiplication, we get
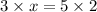
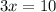
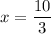
Therefore, the value of x is
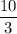 units.
units.