Question

A high school has found over the years that out of all the students who are offered admission, the proportion who accept is 70%.

After the administration has made some changes to the school, they want to check if the proportion of students accepting
has changed significantly. Suppose they offer admission to 210 students and 156 accept. Is this evidence of a change from
the status quo?

Answer 1

The p-value of the test is 0.1738, which means that for a level of significance above this, there is evidence of a change from the status quo.

Explanation:

A high school has found over the years that out of all the students who are offered admission, the proportion who accept is 70%. Test if there is a change from status quo.

At the null hypothesis, we test if the proportion is 70%, that is:

`H_0: p = 0.7`

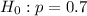
At the alternate hypothesis, we test if there is a change from status quo, that is, the proportion is different from 70%. So

`H_a: p \\eq 0.7`

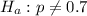
The test statistic is:

`z = (X - \mu)/((\sigma)/(√(n)))`

In which X is the sample mean,
`\mu` is the value tested at the null hypothesis,
`\sigma` is the standard deviation and n is the size of the sample.

70% is tested at the null hypothesis:

This means that
`\mu = 0.7, \sigma = √(0.7*0.3)`

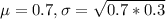
Suppose they offer admission to 210 students and 156 accept.

This means that
`n = 210, X = (156)/(210) = 0.7429`

Value of the test statistic:

`z = (X - \mu)/((\sigma)/(√(n)))`

`z = (0.7429 - 0.7)/((√(0.7*0.3))/(√(210)))`

`z = 1.36`

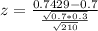
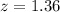
P-value of the test and decision:

The p-value of the test is the probability that the sample proportion differs from 0.7 by at least 0.7429 - 0.7 = 0.0429, which is P(|z| > 1.36), which is 2 multiplied by the p-value of z = -1.36.

Looking at the z-table, z = -1.36 has a p-value of 0.0869

2*0.0869 = 0.1738

The p-value of the test is 0.1738, which means that for a level of significance above this, there is evidence of a change from the status quo.