Question

Vehicles entering an intersection from the east are equally likely to turn left, turn right, or proceed straight ahead. If 50 vehicles enter this intersection from the east, use technology and the normal approximation to the binomial distribution to find the exact and approximate probabilities of the following. (Round your answers to four decimal places.)

a. 15 or fewer turn right.
b. at least two-thirds of those in the sample turn.

Answer 1

a)

0.3632 = 36.32% approximate probability that 15 or fewer turn right.

0.369 = 36.9% exact probability that 15 or fewer turn right.

b)

0.4801 = 48.01% approximate probability that at least two-thirds of those in the sample turn.

0.4868 = 48.68% exact probability that at least two-thirds of those in the sample turn.

Explanation:

Binomial probability distribution

Probability of exactly x sucesses on n repeated trials, with p probability.

Can be approximated to a normal distribution, using the expected value and the standard deviation.

The expected value of the binomial distribution is:

`E(X) = np`

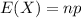
The standard deviation of the binomial distribution is:

`√(V(X)) = √(np(1-p))`

Normal probability distribution

Problems of normally distributed distributions can be solved using the z-score formula.

In a set with mean
`\mu` and standard deviation
`\sigma`, the zscore of a measure X is given by:

`Z = (X - \mu)/(\sigma)`

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.

When we are approximating a binomial distribution to a normal one, we have that
`\mu = E(X)`,
`\sigma = √(V(X))`.

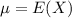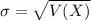Vehicles entering an intersection from the east are equally likely to turn left, turn right, or proceed straight ahead.

This means that
`p = (1)/(3)`

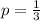
50 vehicles

This means that
`n = 50`

Mean and standard deviation:

`\mu = E(X) = np = 50(1)/(3) = 16.67`

`\sigma = √(V(X)) = √(np(1-p)) = \sqrt{50(1)/(3)(2)/(3)} = 3.33`

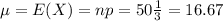
a. 15 or fewer turn right.

Using continuity correction, this is
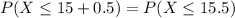`P(X \leq 15 + 0.5) = P(X \leq 15.5)`, which is the pvalue of Z when X = 15.5. So

`Z = (X - \mu)/(\sigma)`

`Z = (15.5 - 16.67)/(3.33)`

`Z = -0.35`

`Z = -0.35` has a pvalue of 0.3632

0.3632= 36.32% approximate probability that 15 or fewer turn right.

Using a binomial probability calculator, to find the exact probability, we get a 0.369 = 36.9% exact probability that 15 or fewer turn right.

b. at least two-thirds of those in the sample turn.

Turn either left or right, so:

`p = (1)/(3) + (1)/(3) = (2)/(3)`

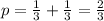
The standard deviation remains the same, while the mean will be:

`\mu = E(X) = np = 50(2)/(3) = 33.33`

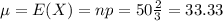
Two thirds of the sample is 33.33, so at least 34 turning, which, using continuity correction, is
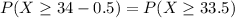`P(X \geq 34 - 0.5) = P(X \geq 33.5)`, which is 1 subtracted by the pvalue of Z when X = 33.5.

`Z = (X - \mu)/(\sigma)`

`Z = (33.5 - 33.33)/(3.33)`

`Z = 0.05`

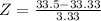
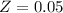
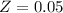`Z = 0.05` has a pvalue of 0.5199

1 - 0.5199 = 0.4801

0.4801 = 48.01% approximate probability that at least two-thirds of those in the sample turn.

Using a binomial probability calculator, we find a 0.4868 = 48.68% exact probability that at least two-thirds of those in the sample turn.