Question

Consider the line x+5y=6

What is the slope of a line perpendicular to this line?

What is the slope of a line parallel to this line?

Answer 1

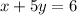`x + 5y = 6` is perpendicular to
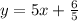`y = 5x + (6)/(5)` and parallel to
`y = -(1)/(5)x + 2\\`

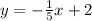
Explanation:

First, convert the equation to standard form so that y is isolated.

x + 5y = 6 --> x - 6 = -5y (divide both sides by -5) -->
`y = -(1)/(5)x + (6)/(5)`

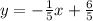
A perpendicular line will have a slope that is the opposite reciprocal of the original slope (meaning you flip the numerator and denominator then make it negative).

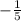`-(1)/(5)` is perpendicular to
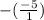`-((-5)/(1) )` which simplifies to 5.

A parallel line will have the same slope, but the y-intercept will be different. It can be pretty much any number as long as the original slope is used in the new equation.

`y = -(1)/(5)x + (6)/(5)\\` is parallel to
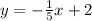`y = -(1)/(5)x + 2\\` just like
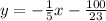`y = -(1)/(5)x - (100)/(23)`.