Question

I need help i dont get it

Answer 1

2) x =
`(5+√(57))/(8)`,
`(5-√(57))/(8)`

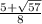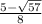
First, you need to begin by rearranging the equation into standard form. This would result to
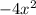`-4x^(2)`+5x+2. Because the first term cannot be a negative, you need to multiply the equation by -1, in order to eliminate the negative. This would result with
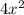`4x^(2)`-5x-2.

There are many different methods when factoring a quadratic equation, including X-Method, Factoring by grouping, GCF, Quadratic Formula, etc. In this case, we will utilize quadratic formula. Quadratic formula is
`(-b±\sqrt b^(2)-4ac)/(2a)`

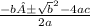
Quadratic equations always follow this variable format:
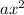`ax^(2)`+bx+c. By using this format, we can use the corresponding numbers to solve the quadratic formula. This would result with
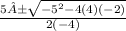`\frac{5±\sqrt{-5^(2)-4(4)(-2)}}{2(-4)}`. Simplify the equation to get
`(5±√(57))/(8)`. (Ignore the A)

10) C

When looking at
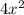`4x^(2)`-5x-2, the leading coefficient would be 4 and the constant would be -2. The middle coefficient would be -5 and the highest degree would be 2. The answer isn't A, because it's true that the degree is less than the number of terms. (There are 3 terms and the degree is 2.) It isn't B, because it's true that -2 is less than 4. It isn't D, because it's true that -2 is less than -5. The answer is C, because the a-value, 4, is not less than the b-value, -5.