Question

A basketball player makes a free throw 82.6% of the time. The player attempts 5 free throws. Use a histogram of the binomial distribution to determine what is the most likely outcome.

Answer 1

The most likely outcome is exactly 4 free throws

Explanation:

Given

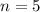`n = 5` --- attempts

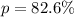`p = 82.6\%` ---- probability of a successful free throw

`p = 0.826`

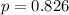
Required

A histogram to show the most likely outcome

From the question, we understand that the distribution is binomial.

This is represented as:

`P(X = x) = ^nC_x * p^x * (1 - p)^(n-x)`

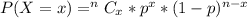
For x = 0 to 5, where x represents the number of free throws; we have:

`P(X = x) = ^nC_x * p^x * (1 - p)^(n-x)`

`P(X = 0) = ^5C_0 * 0.826^0 * (1 - 0.826)^(5-0)`

`P(X = 0) = ^5C_0 * 0.826^0 * (0.174)^(5)`

`P(X = 0) = 1 * 1 * 0.000159 \approx 0.0002`

`P(X = 1) = ^5C_1 * 0.826^1 * (1 - 0.826)^(5-1)`

`P(X = 1) = ^5C_1 * 0.826^1 * (0.174)^4`

`P(X = 1) = 5 * 0.826 * 0.000917 \approx 0.0038`

`P(X = 2) = ^5C_2 * 0.826^2 * (1 - 0.826)^(5-2)`

`P(X = 2) = ^5C_2 * 0.826^2 * (0.174)^(3)`

`P(X = 2) = 10 * 0.682 * 0.005268 \approx 0.0359`

`P(X = 3) = ^5C_3 * 0.826^3 * (1 - 0.826)^(5-3)`

`P(X = 3) = ^5C_3 * 0.826^3 * (0.174)^2`

`P(X = 3) = 10 * 0.5636 * 0.030276 \approx 0.1706`

`P(X = 4) = ^5C_4 * 0.826^4 * (1 - 0.826)^(5-4)`

`P(X = 4) = 5 * 0.826^4 * (0.174)^1`

`P(X = 4) = 5 * 0.4655 * 0.174 \approx 0.4050`

`P(X = 5) = ^5C_5 * 0.826^5 * (1 - 0.826)^(5-5)\\`

`P(X = 5) = ^5C_5 * 0.826^5 * (0.174)^0`

`P(X = 5) = 1 * 0.3845 * 1 \approx 0.3845`

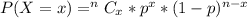
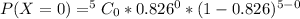
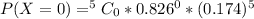
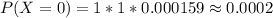
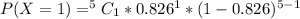
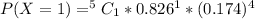
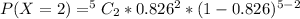
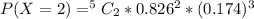
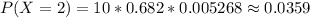
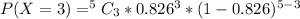
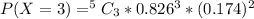
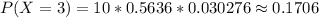
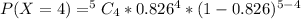
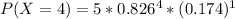
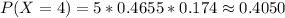
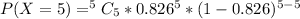
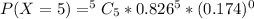
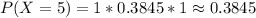
From the above computations, we have:

`P(X = 0) \approx 0.0002`

`P(X = 1) \approx 0.0038`

`P(X = 2) \approx 0.0359`

`P(X = 3) \approx 0.1706`

`P(X = 4) \approx 0.4050`

`P(X = 5) \approx 0.3845`

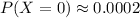
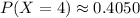
See attachment for histogram

From the histogram, we can see that the most likely outcome is at: x = 4

Because it has the longest vertical bar (0.4050 or 40.5%)