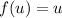Question

This question is designed to be answered without a calculator. Use the antiderivative formula shown, where f(u) represents a function. Integral of (l n u) d u = u ln u – f(u) + C Which function represents f(u)?

Answer 1

`f(u) = u`

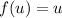
Explanation:

Given

`\int {\ln(u)} \, du = u[\ln(u) - f(u)] + c`

Required

Find f(u)

To do this, we start by integrating the left-hand side

`\int {\ln(u)} \, du = u\ln(u) - f(u)+ c`

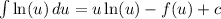
Using integration by parts, we have:

`\int {fg'} = fg - \int f'g`

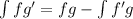
So, we have:

`f = \ln(u)`

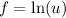
Differentiate

`f'=(1)/(u)`

`g' = 1`

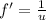
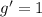
Integrate

`g=u`

So:

`\int {fg'} = fg - \int f'g`

`\int \ln(u)\ du = \ln(u) * u - \int (1)/(u) * u\ du`

`\int \ln(u)\ du = u\ln(u) - \int \ du`

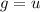
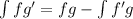
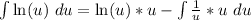
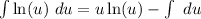
So, we have:

`u\ln(u) - \int \ du = u\ln(u) - f(u) + c`

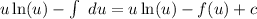
Integrate du using constant rule

`u\ln(u) - u + c = u\ln(u) - f(u) + c`

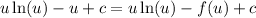
Subtract c from both sides

`u\ln(u) - u = u\ln(u) - f(u)`

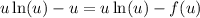
Subtract u ln(u) from both sides

`- u = - f(u)`

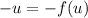
Rewrite as:

`f(u) = u`