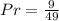Question

The circumference of a circle is 28. Contained in that circle is a smaller circle with area 36π. A point is selected at random from inside the large circle. What is the probability the point also lies in the smaller circle?

Answer 1

`Pr = (9)/(49)`

Explanation:

Given

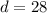`d = 28` --- big circle

`A_2 = 36 \pi` --- area of small circle

Required

Probability that a point selected lands on the small circle

Calculate the area of the big circle using;

`A_1 = \pi r^2`

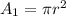
Where

`r = d/2`

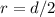
So, we have:

`r = 28/2 = 14`

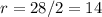
This gives:

`A_1 = \pi * 14^2`

`A_1 = \pi * 196`

`A_1 = 196\pi`

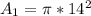
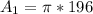
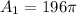
The probability that a point selected lands on the small circle is calculated by dividing the area of the small cicle by the big circle

This gives:

`Pr = (36\pi)/(196\pi)`

`Pr = (36)/(196)`

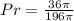
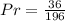
Simplify

`Pr = (9)/(49)`