Question

El tamaño de cierto cultivo de bacterias se multiplica por 2 cada 30 minutos. Si suponemos que el cultivo tiene inicialmente 256 de bacterias, ¿Cuántas bacterias habrá transcurridas 3 horas? Cree un modelo matemático y exprese su respuesta como una potencia

Answer 1

La población de bacterias después de tres horas es de
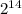`2^(14)` bacterias.

Explanation:

En este enunciado observamos un caso de progresión geométrica, en donde la población de bacterias se duplica cada treinta minutos, es decir:

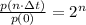`(p(n\cdot\Delta t))/(p(0)) = 2^(n)` (1)

Donde:

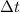`\Delta t` - Intervalo de tiempo requerido para el incremento geométrico de la población, en minutos.

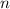`n` - Número de períodos para incremento geométrico, sin unidad.

Sabemos que la población inicial de bacterias es 256 y que 3 horas son 6 veces 30 minutos. Entonces, tenemos la siguiente razón:

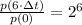`(p(6\cdot \Delta t))/(p(0)) = 2^(6)` (2)

Si sabemos que
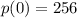`p(0) = 256`, entonces
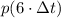`p(6\cdot \Delta t)` es:

`p(6\cdot \Delta t) = 2^(6)\cdot p(0)`

`p(6\cdot \Delta t) = 2^(6)\cdot (256)`

`p(6\cdot \Delta t) = 2^(6)\cdot 2^(8)`

`p(6\cdot \Delta t) = 2^(14)`

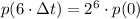
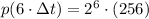
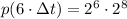
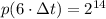
La población de bacterias después de tres horas es de
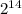`2^(14)` bacterias.