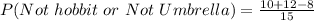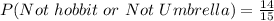Answer:
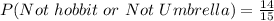
Explanation:
Your question is poorly formatted (See comment section for complete question)
Given
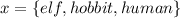 ---- characters
---- characters
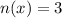
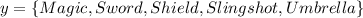 --- tools
--- tools
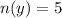
Required
The probability that your character won't be a hobbit or your tool won't be an umbrella?
First we calculate the probability of choosing a hobbit.
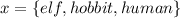
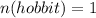
So:
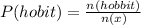
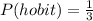
Using the complement rule, we calculate the probability of not choosing a hobbit
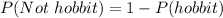
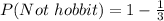

Next, we calculate the probability of choosing an umbrella.
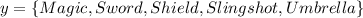
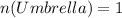
So:
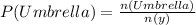
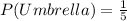
Using the complement rule, we calculate the probability of not choosing an umbrella
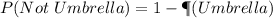
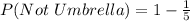
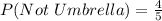
The required probability is calculated using:
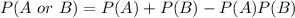
In this case;
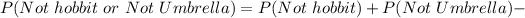
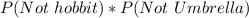
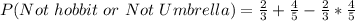
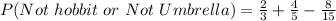
Take LCM