Question

B) A company president would like to offer a 4.00 L cylinder containing 500 g of chlorine in the new catalog. The cylinders you have on hand have a rupture pressure of 40 atm. Use both the ideal gas law and the van der Waals equation to calculate the pressure in a cylinder at 25°C. Given a = 6.58 L2 atm mol-2 and b = 0.056 L mol-2, Cl =35.5. (5 marks)

Answer 1

43.1atm is the pressure using gas law and 27.2atm using Van der Waals Law.

Step-by-step explanation:

Ideal gas law is:

PV = nRT

Where P is pressure in atm

V is volume = 4.00L

n are moles of the gas (For chlorine Molar Mass: 70.90g/mol):

500g * (1mol / 70.90g) = 7.052 moles

R is gas constant = 0.082atmL/molK

T is absolute temperature = 25°C + 273 = 298K

To solve the pressure, P:

P = nRT/V

P = 7.052mol*0.082atmL/molK*298K / 4.00L

P = 43.1atm is the pressure using gas law.

Van der Waals equation is:

`P + a((n)/(V))^2 * (V-nb) = nRT`

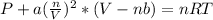
Where a is 6.58L²atm*mol⁻²

b = 0.056Lmol⁻²

Solving for pressure:

`P + a((n)/(V))^2 = (nRT)/((V-nb))`

`P = (nRT)/((V-nb))-a((n)/(V))^2`

`P = (7.052mol*0.082atmL/molK*298K)/((4.00L-7.052mol*0.056L*mol))-6.58L^2mol^(-2)((7.052mol)/(4.00L))^2`

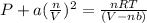
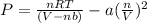
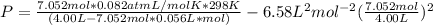
P = 172.323 / 3.6051 - 20.4866

P = 27.2atm using Van der Waals Law