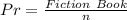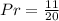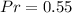Question

The librarian continues to record the type of item that the next 20 patrons check out from the library. patron item type 11 fiction book 12 non-fiction book 13 fiction book 14 fiction book 15 fiction book 16 non-fiction book 17 fiction book 18 non-fiction book 19 fiction book 20 DVD 21 fiction book 22 non-fiction book 23 fiction book 24 fiction book 25 audiobook 26 fiction book 27 DVD 28 non-fiction book 29 fiction book 30 DVD Based on the information from these patrons, estimate the probability that the next patron will check out a fiction book.

Answer 1

`Pr = 0.55`

Explanation:

Given

Represent the dataset with the following frequency table

`\begin{array}{cc}{Item} & {Frequency} & {Fiction\ Book} &{11} & {Non\ Fiction\ Book} & {5} & {DVD} & {3} & {Audiobook} & {1} \ \end{array}`

Required

Probability that the next checkout will be fiction

From the above frequency table, we have:

`Fiction\ Book = 11`

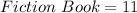
`n =20` --- total

So, the probability that the next checkout item is a fiction book is:

`Pr = (Fiction\ Book)/(n)`

`Pr = (11)/(20)`

`Pr = 0.55`