Answer:
u₂ = 3.7 m/s
Step-by-step explanation:
Here, we use the law of conservation of momentum, as follows:
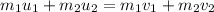
where,
m₁ = mass of the car = 1250 kg
m₂ = mass of the truck = 2020 kg
u₁ = initial speed of the car before collision = 17.4 m/s
u₂ = initial speed of the tuck before collision = ?
v₁ = final speed of the car after collision = 6.7 m/s
v₂ = final speed of the truck after collision = 10.3 m/s
Therefore,

u₂ = 3.7 m/s