Question

Express (x+4)2as an equivalent trinomial. Test the equivalency using x = 1.

Answer 1

`\boxed {\boxed {\sf x^2+8x+16}}`

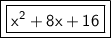
Explanation:

1. Express as an Equivalent Trinomial

To multiply two binomials (expressions with 2 terms), we can use the FOIL (first, outside, inside, last) method.

We are given this expression:

`(x+4)^2`

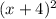
The expression (x+4) is being squared, which is equal to multiplying the term by itself twice.

`(x+4)(x+4)`

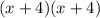
Next, multiply the first terms from both binomials, then repeat for the outside, inside, and last terms.

• First: x*x= x²
• Outside: x*4= 4x
• Inside: 4 *x= 4x
• Last: 4*4= 16

Put the products into one expression.

`x^2+4x+4x+16`

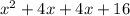
Combine like terms. 4x and 4x both have the variable x, so they can be combined.

`x^2+(4x+4x)+16`

`x^2+8x+16`

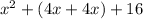
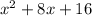
2. Test using x=1

Next, substitute 1 in for x in both the original expression and the trinomial we found. If they are equivalent, the results will be the same.

1. (x+4)²

(1+4)²

(5)² = 25
`\checkmark`

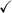
2. x²+8x+16

(1)²+8(1)+16

1+8(1)+16

1+8+16

9+16= 25
`\checkmark`

If x=1, both the original binomial and trinomial equal 25, so we know they are equivalent.