The length of side CD is 6 2/9 feet.
Since the two triangles are similar, we know that the ratio of the corresponding sides is equal. We can set up the following proportion to find the length of side CD:
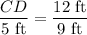
Multiplying both sides of the proportion by 5 ft, we get:
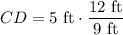
Dividing both sides by 9 ft, we get:
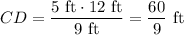
Therefore, the length of side CD is 6 2/9 feet.