Question

Determine the length of the chord that is 8 inches from the center of a circle with a radius of 17 inches?

Answer 1

30 in

Explanation:

See attached image.

The length of AB is 17 (radius). The length of AC is 8 (given info).

AC splits segment BD in half, so point C is the midpoint of segment BD.

AC is perpendicular to the chord, so triangle ABC is a right triangle. You now have a right triangle with a leg of length 8 and hypotenuse of lenght 17.

The Pythagorean Theorem: (leg)^2 + (leg)^2 = (hypotenuse)^2.

`8^2+(BC)^2=17^2\\\\64+(BC)^2=289\\\\(BC)^2=225\\\\BC=√(225)=15`

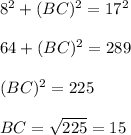
That's half the length of the chord, so double that to get 30 inches for the full length of the chord BD.