Question

On a coordinate plane point M is located at (-6,5) and point N is located at (7,5) what is the distance between point M and point N

Answer 1

The distance between point M and point N is 13.

Explanation:

By Analytical Geometry, we know that straight line distance between two coplanar points can be determined by the Distance Equation of a Line Segment (
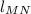`l_(MN)`), which is an application of the Pythagorean Theorem:

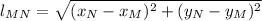`l_(MN) = \sqrt{(x_(N)-x_(M))^(2)+(y_(N)-y_(M))^(2)}` (1)

Where:

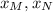`x_(M), x_(N)` - x-Coordinates of points M and N.

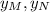`y_(M), y_(N)` - y-Coordinates of points M and N.

If we know that
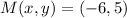`M(x,y) = (-6,5)` and
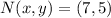`N(x,y) = (7,5)`, then the distance between point M and point N is:

`l_(MN) = \sqrt{[7-(-6)]^(2)+(5-5)^(2)}`

`l_(MN) = 13`

The distance between point M and point N is 13.