Question

For the school fundraiser, a class is selling stationery and greeting

cards. The goal for the class is to sell at least 100 items. The school
receives $2.50 for each stationery set that is sold and $3 for each set
of greeting cards that is sold. The goal is to raise at least $300. Write a
system of inequalities for the given situation and graph the
inequalities.

Answer 1

The system of inequalities is:

`x+y\geq 100\text{ and } 2.5x+3y\geq 300`

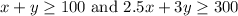
The graphs are provided below as well. The portion where the shaded region intersect are all the possible points.

Explanation:

Let x represent the amount of stationery sets sold, and let y represent the amount of greeting sets sold.

The goal is to sell at least 100 items. So, the sum of x and y should be at least 100. In other words:

`x+y\geq 100`

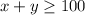
Another goal is to raise at least $300. Since each stationery set sells for $2.50 and each greeting set sells for $3.00, we can write:

`2.5x+3y\geq 300`

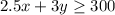
So, our system of inequalities is:

`x+y\geq 100\text{ and } 2.5x+3y\geq 300`

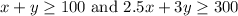
To graph, we can first graph them as lines. Rewrite the equations:

`\displaystyle y\geq 100-x`

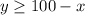
And:

`\displaystyle 3y\geq 300-(5)/(2)x \Rightarrow y\geq 100-(5)/(6)x`

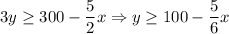
Ignore the inequalities and graph the lines. This is shown in the first graph below.

Both inequalities have "or equal to," so we have solid lines.

Finally, since both inequalities have y as "greater than" the equation, our shaded portion will be above the lines. This is shown in the second graph. The portion where both shaded regions covers are all the feasible points.